棒グラフ、円グラフ、ヒストグラム……データを分かりやすく表示するために用いられるグラフにはさまざまなものがあります。そのひとつ、箱ひげ図を普段から使っているという人はそれほど多くないのではないでしょうか。
しかし、箱ひげ図はデータの散らばり具合を直感的に把握することに適しており、まずデータをざっくり把握して問いを立てたいという方にぜひおすすめしたいグラフです。
本記事では、箱ひげ図の見方・書き方・使い方についてわかりやすくご紹介します！
箱ひげ図とは、データの分布を「箱」と「ひげ」で表したグラフです。データがどこの値に位置しているのかを簡単に把握できます。 データのばらつきであればヒストグラムでも把握できますが、箱ひげ図の場合は異なる複数のデータのばらつきを比較できる特徴があります。
さて、“データのばらつき”を把握するために箱ひげ図と並んでよく用いられるのが「ヒストグラム」です。では箱ひげ図とヒストグラムはどう違うのでしょうか？
大きな違いが、複数のデータ群のざっくりとした比較に向いているのか、単一のデータの度数分布の把握に向いているのかという点。
28日間でA～Eの5会場に訪れた来場者数を1日ごとに計測したデータを例として考えましょう。
箱ひげ図は以下のように、複数のデータのばらつき具合を比較できます。Ａ会場の来場者数が8,000～10,000人の間に収まり他会場と比べて人気があること、B・C・D会場の来場者数はおおむね4,000～6,000人の間に収まり似通っていること、E会場の来場者数データのばらつきは大きいこと等が一目で伝わりますね。
一方、日本語で度数分布図とも言い表されるヒストグラムは、ひとつのデータをある幅ごとに区切り、その散らばりぐあいや確率分布への当てはまりを確かめるために用いられます。
M-1グランプリ2001～2020の得点分布の経年変化について解説するデータのじかんの記事でも、以下のように複数のデータ群を比較するために、箱ひげ図が用いられています。
引用元：M-1グランプリ2020年大会をデータで観察。今年の特徴は「最低点が最高点」？┃データのじかん
外れ値とは、データの中で他の値から大きく外れている値のことを指します。通常、外れ値は最大値や最小値として扱わず、箱ひげ図の外に表示されます。外れ値を最大値や最小値として扱うと、データのばらつきを正しく把握できなくなるため、ヒゲが異常に長くなってしまいます。
しかし、極端に他の値から離れている値を感覚だけで判断することはできません。箱ひげ図では、第1四分位数や第3四分位数から四分位範囲の1.5倍以上離れた値を外れ値と定義しています。この方法を使えば、明らかに他の値から離れている値を特定し、データセットから取り除くことができます。
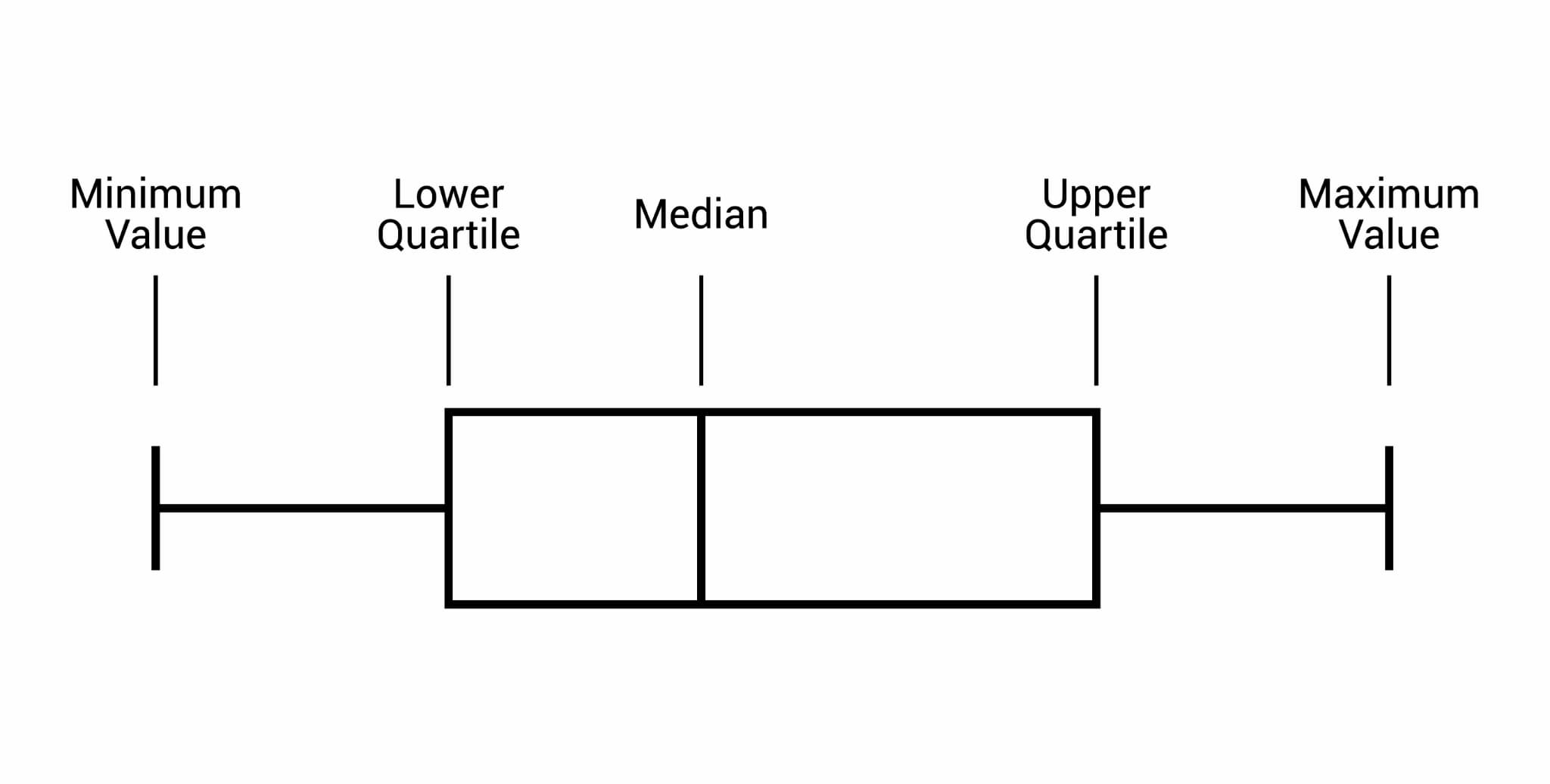
早速ですが、まずは箱ひげ図のサンプルをご覧ください。
ご覧の通り、箱ひげ図ではデータの「最大値」「最小値」「第1四分位数」「中央値（第2四分位数）」「第3四分位数」「平均値」「外れ値」を表すことができます。
統計ではデータのばらつきを把握するために、数値の小さい方から4つに分割する四分位数がよく用いられます。「第1四分位数」は25％値、「中央値（第2四分位数）」は50％値、「第3四分位数」は75％値とも言い換えられます。第3四分位数と第1四分位置数の差を「四分位範囲」といい、四分位範囲が大きいほど、データの散らばりが大きいと考えられます。
中央値はデータ全体を下から並べた場合の真ん中（50％）であり、多くの方にとってなじみ深い平均値はデータの合計をデータの個数で割って均した値です（基礎的な統計用語について詳しくはコチラ）
平均値は他のデータに比べて極端に大きい、あるいは小さい外れ値の影響を受けやすく、中央値は受けにくいという特徴があります。なお、×で表される平均値については箱ひげ図では書き込まれていないことも多いです。
箱ひげ図は1970年代にアメリカの数学者・統計学者のジョン・W・テューキー（1915-2000）によって考案されました。FFTアルゴリズムの開発や今では当たり前に使われているデジタル用語“ビット”の考案など多くの功績を残したテューキー。彼が提唱したのが、多角的な視点でデータを捉え、“モデルありき”でなく構造を理解することを重視する「探索的データ解析（EDA：Explanatory Data Analysis）」です。
データを正しく解析し、実務に結び付けることを重視したテューキー考案の箱ひげ図は、まさにデータの特徴を直感的に理解することに適したツールだといえるでしょう。
箱ひげ図を実際に自分でもつくってみたい、という方に朗報です。実は2016以降のバージョンのExcelには標準で箱ひげ図を作成する機能が備わっているので、割と簡単に箱ひげ図を作成することができます。
その手順は、以下の通り。
※この際選択するのは、分析対象となる数値データのセルのみ
また、データ分析関連で注目度の高いプログラミング言語Pythonではpandasライブラリの「plot.box()」関数で箱ひげ図を作成することが可能です。
※GoogleColaboratoryで筆者作成の上、キャプチャ
箱ひげ図の基本的な見方・使い方・書き方について解説いたしました。思った以上に簡単でデータ活用初心者にも優しいツールだと驚かれたのではないでしょうか？
ぜひ今後データの特徴をざっくりと把握したいと思ったときは、「箱ひげ図」の存在を思い出してみてください。積極的に使ってみることでデータを扱う視点がより大きく広がるはずです！
（宮田文机）
・栗原 伸一 (著), 丸山 敦史 (著), ジーグレイプ 制作『統計学図鑑 (日本語) 単行本（ソフトカバー）』オーム社、2017
・箱ひげ図の見方・書き方を解説！一瞬で伝わるレポート資料の作り方┃ferret
・Who think boxplot！箱ひげ図が誕生した経緯に迫る┃ferret
・第1回データ解析の第一歩は計算ではない┃実験医学online
・探索的データ解析（Exploratory data analysis)とは？┃NTTデータ数理システム
・ヒストグラムとは？ヒストグラムの書き方(作り方)や分布図の見方を徹底解説┃backlogブログ
メルマガ登録をしていただくと、記事やイベントなどの最新情報をお届けいたします。
30秒で理解！インフォグラフィックや動画で解説！フォローして『1日1記事』インプットしよう！
