相関関係とは、2つの事柄が関わり合う関係のことであり、特に統計学では一方の数値が増加すると、もう一方の数値が減少または増加する関係のことをいいます。例えば、雨が降れば、その地域の川の水量は増加します。このように一方が増えると、もう一方も増える状態を正の相関関係といいます。逆に、地球全体の気温が上がれば、北極や南極の氷の量は減ります。このように一方が増えるともう一方が減少する状態を負の相関関係といいます。
相関関係とは、一方が増えることでもう一方が増加または減少する状態を指すだけであり、それだけで2つの事象に因果関係があると判断できるものではありません。因果関係を証明するには、相関関係を示した上で、別の方法で因果を証明する必要があります。
また、因果関係は「ある/ない」と表現されることが多いのですが、相関関係の場合は「強い/弱い/ない」と表現されることが多いです。
それでは、どのような状態の場合に相関関係が強かったり、弱かったり、なかったりするのでしょうか。
そもそも、相関が強いというのはどういうことなのでしょうか。相関が強くても、弱くても、一方が増えればもう一方が増える、もしくは減る傾向にあることには変わりありません。ただし、相関が弱いと、もう一方の増え方が大きかったり、小さかったりとバラつきがある状態となります。
相関が強いか弱いかを示す数値に、相関係数という数値があります。この相関係数の数値の大小で相関が強いか弱いかがわかります。諸説ありますが、相関係数の大小と相関の強弱の関係は以下が目安とされています。
| 0.7 ~ 1.0 | かなり強い正の相関がある |
| 0.4 ~ 0.7 | 正の相関がある |
| 0.2 ~ 0.4 | 弱い正の相関がある |
| -0.2 ~ 0.2 | ほとんど相関がない |
| -0.4 ~ -0.2 | 弱い負の相関がある |
| -0.7 ~ -0.4 | 負の相関がある |
| -1.0 ~ -0.7 | かなり強い負の相関がある |
相関の強弱を具体的な表とグラフで見てみましょう。下の表は、架空のアイス屋の8月1日から8月10日のアイス販売個数と気温の表です。
| 日付 | 気温 | 販売個数 |
| 8/1 | 20 | 20 |
| 8/2 | 21 | 32 |
| 8/3 | 30 | 50 |
| 8/4 | 25 | 30 |
| 8/5 | 27 | 56 |
| 8/6 | 33 | 62 |
| 8/7 | 25 | 50 |
| 8/8 | 26 | 47 |
| 8/9 | 27 | 25 |
| 8/10 | 28 | 36 |
気温とアイスの売上と聞けば、きっと多くの人は「暑いとアイスはよく売れる」と考えると思います。しかし、この表だけでは「暑いとアイスはよく売れる」と言えるかはよくわかりません。そこで、X軸を気温、Y軸を販売個数にして散布図にしたのが以下のグラフとなります。
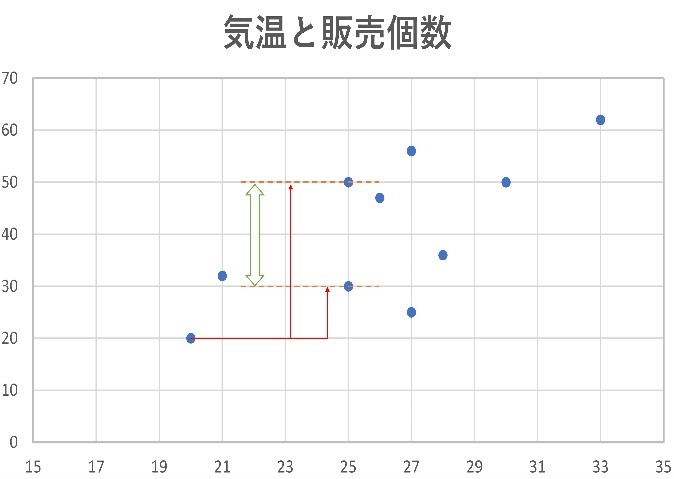
架空のアイス屋の気温と販売個数の散布図(著者作成)
このグラフを見ると、やはり「暑いとアイスはよく売れる」といえそうです。このグラフの相関係数は0.7です。計算方法は後ほど説明しますが、「相関がある」と「強い相関がある」の間くらいの数値です。
グラフを見ると、8月1日は気温20℃で20個が売れていますが、そこから5℃気温が上がった25℃の日を見てみると、30個売れた日もあれば50個売れた日もあります。これくらいのバラつきがあるのが、相関係数が0.7の相関関係ということになります。
同じような条件で、相関係数が0.9、0.2となるような散布図を作成すると、以下のようになります。
相関係数 0.9 ほとんどバラつきがない
相関係数が0.9の気温と販売個数の散布図(著者作成)
相関係数 0.2 バラついて相関がありそうに見えない
相関係数が0.2の気温と販売個数の散布図(著者作成)
0.9の相関係数は、目安として「かなり強い」相関があります。この場合は、ほぼバラつきがありません。一方、相関係数が0.2のグラフは、アイスの販売個数と気温にはほとんど関係がないように見えます。目安としてはギリギリ「弱い相関」があるグラフですが、ここまでバラつきがある状態です。相関の強弱は、このバラつきの有無といえます。
それでは、前述の相関関係の強さを表す相関係数の求め方ですが、手計算や電卓で計算する場合には、次のような公式で求めることができます。
(相関係数)=((共分散))/((Xの標準偏差)×(Yの標準偏差))
共分散や標準偏差について説明を始めると数学のテキストになってしまうので、ここでは割愛します。その代わりに、簡単に相関係数を求める方法を以下に記載します。どちらもエクセルを使います。
エクセルでは、相関係数をダイレクトに計算してくれる関数があります。それがCORREL関数です。下記のように、CORREL関数の中に、X軸とY軸の値を入れれば、そのまま相関係数を計算してくれます。
CORREL関数の使用方法(著者作成)
2つ目の方法は、散布図を作って近似曲線を表示し、オプションで相関係数の2乗を表示させる方法です。エクセルで散布図を作り、任意のグラフの点を右クリックすると、近似曲線が引けます(今回の例では、直線になっています)。
この直線は、散布された全ての点から、一番離れないように引いた線です。この線のオプションに「グラフにR-2乗値を表示する」というチェックボックスがあるので、チェックするとグラフ上に相関係数を2乗した値が表示されます。
なぜ2乗なのかは割愛しますが、この値を元にSQRT関数か電卓のルートを使って平方根を求めれば、相関係数を求めることができます。相関係数の正負は適宜判断してください。ついでに「グラフに数式を表示する」にもチェックをしておくと、近似曲線の式が表示されるため便利です。
散布図から相関係数を求める方法(著者作成)
相関の意味と相関係数の求め方については上記の通りですが、身の回りにあるデータを使って実際に相関係数を計算するとどのような結果になるかをご紹介します。今回は、インターネット上で取得できるオープンデータから相関を計算しました。
先程は架空のアイスクリーム屋で相関を計算してみましたが、リアルなデータではどうなのかを計算してみました。とはいえ、アイスクリーム屋の販売データは取得できなかったので、アイスの生産量で計算してみました。
総務省統計局には日本の様々な統計データが収集されており、年別の全国のアイスクリーム生産量のデータがありました。気温については「日本の気温」というのは存在しないので、東京の8月の平均気温を利用しました。どちらも、以下のURLから取得可能です。
・e-Stat 牛乳乳製品の生産動向 速報 牛乳乳製品の生産動向 https://www.e-stat.go.jp/dbview?sid=0003445862 ・気象庁 東京 日平均気温の月平均値(℃) https://www.data.jma.go.jp/obd/stats/etrn/view/monthly_s3.php?prec_no=44&block_no=47662
東京8月平均気温とアイス生産量(著者作成)
X軸が東京の8月の平均気温で、Y軸が年間アイスクリーム生産量(千kl)です。R2乗が0.122なので相関係数は0.35となり、弱い相関があるといえます。全国の生産量と東京の気温との関係を見たので、そこまで強い相関はありませんでした。全国の生産量ではなく東京の販売量データがあれば、もう少し強い相関が見られたかもしれません。
都道府県の人口と婚姻率、離婚率に関係があるかを見てみましょう。こちらは総務省統計局からデータ取得ができました。
・総務省統計局
https://www.stat.go.jp/data/nihon/02.htm
今回は令和2年(2020年)時点の、各都道府県の人口を利用しました。結婚率については、その年の婚姻件数を都道府県の人口で割ることで求めました。離婚率も同様です。
人口と婚姻率(著者作成)
人口と離婚率(著者作成)
著者は当初、人口と婚姻率については負の相関があるかと予想していました。つまり、人口が多い都道府県ほど、婚姻率は低いのではないかと思ったのです。しかし、予想に反して、相関係数は0.67で正の相関がありました。人口が多い都道府県ほど、婚姻率が高いようです。
また、離婚率については、こちらについても予想とは異なり、相関がないことが分かりました。このような結果となった理由については、もう少し想像の翼を広げる必要がありそうです。
次は、消防吏員と火事件数の関係です。消防吏員とは、消防署職員や消防団員等、消火活動に従事する人のことです。火事件数共に、消防白書から取得しました。
・令和4年 消防白書
https://www.fdma.go.jp/publication/ugoki/2022/
火事件数と消防吏員数(著者作成)
上の図は都道府県別の結果で、X軸が火事件数で、Y軸が消防吏員数です。相関係数は0.98と、強い相関がみられました。火事の多い都道府県は、消防吏員数も多いという調査結果となりました。
ただし、今回のケースは疑似相関を疑う必要があります。火事が多いのも消防吏員数が多いのも、人口が多いからではないかという可能性が考えられます。詳細は割愛しますが、火事の件数と消防吏員数から人口の影響を除外して改めて相関を計算することもできます。このように第3の因子(例:人口)の影響を除いた相関係数を偏相関係数と言います。
残差火事件数と残差消防吏員数(著者作成)
観測値(実際の火事件数と消防吏員数)から人口から理論的に算出される予測値(火事件数と消防吏員数)をそれぞれ差し引いた値を残差と言います。観測値より予測値が大きくなることもあるので、残差はマイナスも出てきてしまいます。この残差は、人口の影響を除外した、火事件数と消防吏員数といえます。その残差同士の相関係数が偏相関係数となります。偏相関係数の公式とは異なりますが、結果は同じ値になります。今回の場合の偏相関係数は0.36で、弱い相関がみられます。人口の影響を除外しても、消防吏員数は火事の件数にある程度は応じて配備されているということがわかります。
最後は著者の趣味である歴史分野の分析です。江戸時代は石高が高い藩ほど江戸から離れたい場所にあるというイメージがあったのですが、それが本当か調べてみました。江戸時代の紳士録と呼ばれた武鑑全集を、データベース化してオープンデータにしているサイトがあったので、そこからデータを取得しました。こちらは武鑑全集だけでなく、いろいろな人文学系のデータをオープンデータにしている興味深いサイトです。
・人文学オープンデータ共同利用センター 武鑑全集
http://codh.rois.ac.jp/bukan/
江戸からの距離と石高(著者作成)
X軸は各藩の藩庁から江戸城までの直線距離です。単位は1緯度(経度)分です。Y軸が藩の石高です。計算するまでもなく相関はないようです。
本稿では相関関係の意味や強弱について説明してきました。データさえあれば、相関はエクセルで簡単に求めることができます。また、本稿で紹介したe-Statの他にも、たくさんのオープンデータが存在しています。気になることがあれば、データを入手し、相関を調べてみると、新たな発見につながるかもしれません。ぜひ試してみてください。
藤田 哲久(ふじた・てつひさ)氏
都内SIer勤務。中小企業診断士。統計学に興味を持ち始め、勉強中。統計検定2級、データサイエンス基礎取得。習得した知識を、本業や診断士活動に活用できないか模索中。
データサイエンスの自学自主を支援するパラレルキャリア研究会所属
メルマガ登録をしていただくと、記事やイベントなどの最新情報をお届けいたします。
30秒で理解!インフォグラフィックや動画で解説!フォローして『1日1記事』インプットしよう!
データ越境者に寄り添うメデイア「データのじかん」が提供する便利ツールです。
本ツールは、JavaScriptを用いてお客様のブラウザ上で処理を行います。サーバーとの通信は行われず、入力データはお客様のみの端末内で処理されます。