データのじかんではデータドリブンを奨励しているわけですが、私たちが住んでいるこの世界には実はデータや数字にまつわるたくさんの不正が潜んでいます。

たとえばそれは、インスタグラムのフォロワー数やYouTuberの登録者数という身近なものから、株価や企業の粉飾決済といった、その国の経済に大きく影響を及ぼすものまでありとあらゆる形で存在しているのです。

ずる賢い人々は、あの手この手を使ってこうした不正を日夜行っているわけですが、実は、そういった不正を暴くために使われているとある法則があります。　

それが今回ご紹介する「ベンフォードの法則」です。

「ベンフォードの法則」とは

ベンフォードの法則とは、自然界に現れる数字の最初の桁は「1」が最も多く、「2」「3」と大きくなるにつれ出現する確率は減少し、「9」から始まる数字は最も出現する確率が低くなることを示す法則です。これをグラフで表すと以下のようになります。

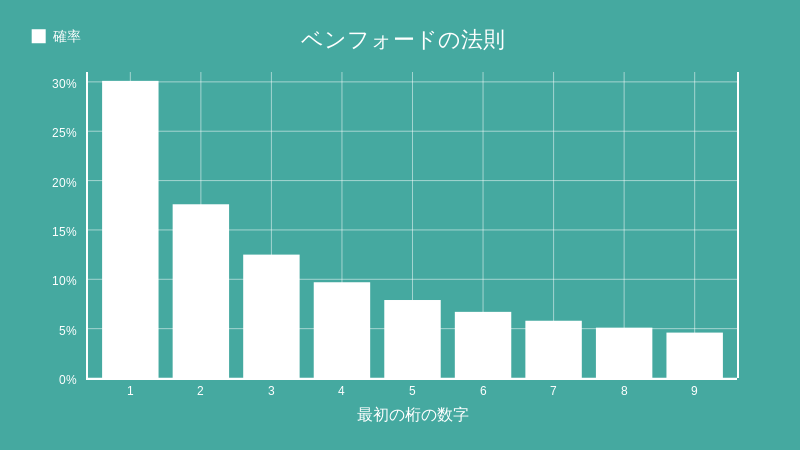
「1」から始まる数字が出現する確率がおよそ30%であることに対して、「2」はおよそ17%と急激に減り、「9」にいたっては5%以下であるといいます。この法則は郵便番号、川の長さ、ガス代、死亡率などなど、様々なデータにおいて見ることができます。たとえば、適当な新聞を用意して、その中に出現する数字をすべて集計してみても、このグラフのようになってしまうのです。

この法則は1881年にアメリカ人の天文学者サイモン・ニューカムによって発見されました。当時は計算をするために対数表というものが使用されていたのですが、ある時彼は1で始まる数値が記載されているページは他の数値で始まるページよりも使用頻度が高いことに気がつきました。ニューカムの法則と呼ばれていても不思議はなさそうですが、この法則は物理学者のフランク・ベンフォードによって1938年に再発見され、法則の名前はベンフォードの法則と名付けられました。

なぜこの法則が成立するのか。

直感的には自然に存在する数字にそんな法則があるはずもなさそうに感じてしまいますが、この法則が成立するための根拠というか、理由づけもちゃんと存在します。

ベンフォードの法則が当てはまるデータの重要な要素として、「時間の経過とともに増加していくか否か」という要素があります。

たとえば、ツイッターのフォロワーで考えてみましょう。ツイッターのフォロワーを0人から10人獲得するまでの時間は、20人獲得するまでの時間と比べて短時間で済むということはわかりますよね。これが20人獲得する時間より30人、30人より40人……というようにして、90人になるのは最も時間がかかります。そしてしばらく経ってフォロワーが100人になったとします。次は桁が一つ上がって100人単位で考えます。100人獲得するまでの時間よりも、200人獲得する時間の方が長い。200人よりも…。というように、これが1000人、10000人とすべての桁においてベンフォードの法則が成り立ちます。これが積み重なっていくことで、先ほどのグラフのようになっていくのです。この例と同じようにして、時間とともに増加する数値はすべてこの法則にあてはまると言われています。

では、この法則を用いて、どのようにフォロワー数の不正を検証するのでしょうか。たとえば、Aさんがツイッターのアカウントを所有しているとして、500人のフォロワーがいるとします。さらにその500人のフォロワーそれぞれのフォロワーの数を集計すると、これはベンフォードの法則に従った形のグラフになります。このとき、もし仮にこの法則に従わない形のグラフになった場合、Aさんは何かしらの不正を働いている可能性が高いということになるのです。

このようにして、ベンフォードの法則を用いて次々と不正を暴く、ということができたら良いのですが、実際にはすべてのデータ群に当てはまる訳ではありません。たとえば携帯電話の番号や銀行の口座番号など、ある特定のルールによってその数字が定められている場合、この法則を用いることはできません。このあたりの見極めが非常に難しく、この法則を用いる際に注意しなければならない点でもあります。たとえば、一見ベンフォードの法則に従うように思える「選挙の得票数」ですが、必ずしもベンフォードの法則に当てはまるわけではないようです。実際に2020年のアメリカ大統領選挙では、このベンフォードの法則が大きな問題の火種となりました。

バイデン氏の不正をベンフォードの法則が暴く？

今回の2020年大統領選挙では、敗北した共和党のトランプ氏が「民主党のバイデン氏が選挙で不正を行ったため、今回の選挙は無効である」と主張して大きな話題となりました。その発言に勢いをつける形でSNSに投稿され始めたのが、公開されている得票数のデータがベンフォードの法則に従うかどうか検証するグラフでした。（たとえばこの投稿）

確かにいくつかの州が公開している開票情報を見ると、バイデン氏の得票数のグラフはトランプ氏のグラフと比べて法則に従っていないため、バイデン氏が何らかの不正を働いたのでは？と考える人がいても不思議ではありません。

ですが、彼らが用いている選挙の得票数のデータは、ベンフォードの法則に従わないことがわかっています。なぜでしょうか。それにはいくつか理由があります。

一つ目の理由として、アメリカにおける選挙のシステムそのものがあげられます。アメリカは民主党と共和党の二大政党です。そのため、ほぼすべてのアメリカ国民は選挙の際、民主党か共和党に票を投じることになります。これはつまり、どちらかの党の得票数が決定すれば、自動的にもう片方の党の得票数が決定されてしまうことを意味します。データが何かしらの数値の影響を受けている場合、それはベンフォードの法則には従いません。これが、ベンフォードの法則に当てはまらない理由の一つです。

二つ目の理由として、共和党と民主党の支持率が均衡していたということがあります。アメリカの大統領選挙は、州ごとに得票数が開示されます。それぞれの州の総人口はベンフォードの法則に従って「1」から始まります。1から始まる場合で支持率が均衡している場合を考えると、それぞれの州の得票数が「4」「5」「6」から始まる数字になることが予想されます。そのため、今回の大統領選挙の結果をそのままこの法則に当てはめることはできないのです。

結論としては、少なくともベンフォードの法則では、バイデン氏が今回の選挙で不正をしたかは証明できないということです。

まとめ

世界の不正を暴く魔法のツール「ベンフォードの法則」。万能ではないとはいえ、数値の出現確率に関する一つの法則が、数多の自然現象だけではなく、企業の決済情報からSNSのフォロワー数のような数字にまで一貫して適応することができると考えると、まるで世界が絶対的な存在にデザインされているのではないかとわくわくしてしまいます。

もっと詳しく知りたいと思った方は、文系の方でもわかりやすいように解説されている永野裕之さんの『とてつもない数学』がおすすめです。

【参考URL】
・Wikipedia-ベンフォードの法則
・Netflix-ビッグデータ黄金時代: 世界の繋がりを科学する
・Benford’s law and the 2020 US presidential election: nothing out of the ordinary
・Benford’s Law Does Not Prove Fraud in the 2020 US Presidential Election
・Fact check: Deviation from Benford’s Law does not prove election fraud

（織田哲平）